\( n \) を \( 2\) 以上の自然数とする。
(1) \( 0 \le x \le 1 \) のとき、次の不等式が成り立つことを示せ。
\begin{equation}
\frac{1}{2}x^n \le (-1)^n \left\{ \frac{1}{x+1}-1-\sum^n_{k=2}(-x)^{k-1} \right\} \le x^n – \frac{1}{2}x^{n+1}
\end{equation}
(2)\( \displaystyle a_n = \sum^n_{k=1}\frac{(-1)^{k-1}}{k} \) とするとき、次の極限値を求めよ。
\begin{equation}
\lim_{n \rightarrow \infty} (-1)^n n ( a_n – \log 2 )
\end{equation}
【解説】
(1)は等比数列の和の公式を使い、\( \sum\) を計算しましょう。
初項 \(a\)、公比 \(r\) の等比数列 \( \{ a_n \} \) の和 \(S_n \)
\begin{equation}
S_n =
\left\{
\begin{array}{ll}
\displaystyle a \cdot \frac{r^n-1}{r-1} & (r \ne 1) \\
na & (r=1) \\
\end{array}
\right.
\end{equation}
(2)では(1)の結果を使います。はさみうちの原理ですね。ただ\(x\) を消去しなければなりません。\( 0\le x \le 1 \) の区間で(1)の各辺の定積分を計算します。
【解答】
(1)
\begin{eqnarray}
&& (-1)^n \left\{ \frac{1}{x+1}-1 – \sum^n_{k=2}(-x)^{k-1} \right\} \\
&& = (-1)^n \left\{ \frac{1}{x+1}-1 – (-x) \frac{1-(-x)^{n-1}}{1-(-x)} \right\} \\
&& = (-1)^n \left\{ \frac{1}{x+1}-1 + \frac{x+(-x)^{n}}{x+1} \right\} \\
&& = \frac{(-1)^n(-x)^n}{x+1} \\
&& = \frac{x^n}{x+1} \cdots ①
\end{eqnarray}
よって
\begin{equation}
\frac{1}{2}x^n \le \frac{x^n}{x+1} \le \left(1-\frac{x}{2} \right)x^n \\
\frac{1}{2} \le \frac{1}{x+1} \le 1-\frac{1}{2}x \cdots ② \\
(∵x^n>0)
\end{equation}
を示ばよい。
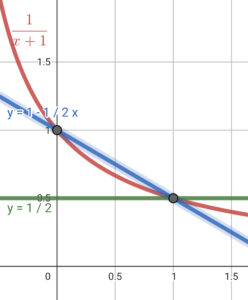
グラフから \( 0 \le x \le 1 \) において②が成り立つので、以下も成り立つ。
\begin{equation}
\frac{1}{2}x^n \le (-1)^n \left\{ \frac{1}{x+1}-1-\sum^n_{k=2}(-x)^{k-1} \right\} \le x^n – \frac{1}{2}x^{n+1} \cdots ③
\end{equation}
(2)
\begin{equation}
f_n(x) = (-1)^n \left\{ \frac{1}{x+1}-1 -\sum^n_{k=2}(-x)^{k-1} \right\}
\end{equation}
とおく。
\begin{eqnarray}
&& \int_0^1 f_n(x) dx \\
&& = (-1)^n \left\{ \int_0^1 \left(\frac{1}{x+1}-1 \right)dx – \sum_{k=2}^{n}\int_0^1 (-x)^{k-1}dx \right\} \\
&& = (-1)^n \left\{ \left[ \log|x+1|-x \right]_0^1 – \sum_{k=2}^n \int_0^1(-1)^{k-1}x^{k-1}dx \right\} \\
&& = (-1)^n \left\{ \log2-1 -\sum_{k=2}^{n}(-1)^{k-1} \left[\frac{1}{k}x^k \right]_0^1 \right\} \\
&& = (-1)^n \left\{ \log2-1 -\sum_{k=2}^{n}(-1)^{k-1} \cdot \frac{1}{k} \right\} \\
&& = (-1)^n \left\{ \log2 -\sum_{k=1}^{n} \frac{(-1)^{k-1}}{k} \right\} \\
&& = (-1)^n ( \log2 – a_n ) \\
&& = -(-1)^n ( a_n – \log2 ) \cdots ④
\end{eqnarray}
ここで③より
\begin{equation}
\frac{1}{2}x^n \le f_n(x) \le x^n – \frac{1}{2}x^{n+1} \\
\int_0^1\frac{1}{2}x^n dx \le \int_0^1 f_n(x)dx \le \int_0^1 \left( x^n – \frac{1}{2}x^{n+1} \right) dx \cdots ⑤
\end{equation}
ここで
\begin{eqnarray}
(⑤の左辺) &=& \left[ \frac{1}{2(n+1)}x^{n+1} \right]_0^1 \\
&=& \frac{1}{2(n+1)} \\
(⑤の右辺)&=& \left[ \frac{1}{n+1}x^{n+1} -\frac{1}{2(n+2)}x^{n+2} \right]_0^1 \\
&=& \frac{1}{n+1}-\frac{1}{2(n+2)}
\end{eqnarray}
だから
\begin{equation}
\frac{1}{2(n+1)} \le -(-1)^n ( a_n – \log2 ) \le \frac{1}{n+1} – \frac{1}{2(n+2)} \\
\frac{n}{2(n+1)} \le -(-1)^n n ( a_n – \log2 ) \le \frac{n}{n+1} – \frac{n}{2(n+2)} \\
\frac{1}{2 \left( 1+\frac{1}{n} \right) } \le -(-1)^n n ( a_n – \log2 ) \le \frac{1}{1+\frac{1}{n}} – \frac{1}{2 \left( 1+\frac{2}{n} \right) } \\
\end{equation}
\( n \rightarrow \infty \) のとき、左辺、右辺ともに \( \displaystyle \frac{1}{2} \) に収束するので、はさみうちの原理から、
\begin{equation}
\lim_{n \rightarrow \infty} (-1)^n n ( a_n – \log2 ) = – \frac{1}{2} \cdots (答)
\end{equation}


