\(O\) を原点とする \(xyz\) 空間において、点 \(P\) と点 \(Q\) は次の \(3\) つの条件 \((a), (b), (c) \) を満たしている。
(a) 点 \(P\) は \(x\) 軸上にある。
(b) 点 \(Q\) は\(yz\) 平面上にある。
(c) 線分 \(OP\) と線分 \(OQ\) の長さの和は \(1\) である。
点 \(P\) と点 \(Q\) が条件 \((a), (b), (c) \) を満たしながらくまなく動くとき、線分 \(PQ\) が通過してできる立体の体積を求めよ。
解説
求める体積は \(x\) 軸について対称な図形となります。平面 \(x=k\) で切ったときの切り口の円の半径を求めましょう。
解答
点\(P\) の \(x\) 座標を \( t\ (0 \lt t \lt 1 ) \) とおくと、\(OQ=1-OP=1-t \)。平面 \( x=k \) と \(PQ \) との交点を \( R_1 \)、\(x\) 軸との交点を \( R_0 \) とする。\(R_0R_1 \) の長さを \( r(k)\) とする。
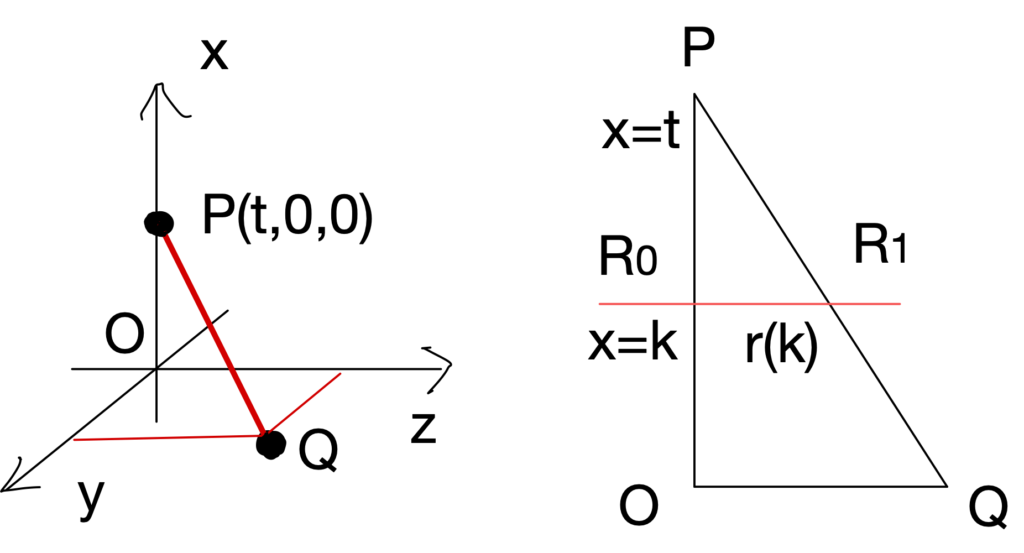
\( \triangle POQ ∽ \triangle PR_0R_1 \) だから
\begin{equation}
PO:PR_0=OQ:R_0R_1 \\
t:t-k=1-t:r(k)\\
∴ r(k) = \frac{(1-t)(t-k)}{t} \\
= (1-t) \left( 1-\frac{k}{t} \right) \\
ただし k \lt t \lt 1
\end{equation}
ここで \(t\) が動くときの \(r(k)\) の最大値を考える。
\begin{eqnarray}
r(k) && = R(t) = (1-t) \left( 1-\frac{k}{t} \right) \\
&& = 1-\frac{k}{t}-t+k \\
R^{\prime}(t) && = -1+\frac{k}{t^2} \\
&& = – \frac{ \left( t-\sqrt{k} \right) \left( t+\sqrt{k} \right) }{t^2} \\
\end{eqnarray}
\(R^{\prime}(t)=0 \) とすると \( t=\pm \sqrt{k} \)
\begin{array}{c|ccccc}
t & k & \cdots & \sqrt{k} & \cdots & 1 \\
\hline
R^{\prime}(t) & & + & 0 & – & \\
\hline
R(t) & & \nearrow & 極大 & \searrow & \\
\end{array}
\begin{eqnarray}
R(\sqrt{k}) && = (1-\sqrt{k}) \left( 1-\frac{k}{\sqrt{k}} \right) \\
&& = (1-\sqrt{k})^2
\end{eqnarray}
求める立体 \(V\) と \( x=k \) の切り口は半径 \( R(\sqrt{k}) \) の円となる。また求める体積は \(xy\) 平面で対称だから、
\begin{eqnarray}
V && = 2\int_0^1 \pi \left\{ R(\sqrt{k}) \right\}^2 dk \\
&& = 2\pi \int_0^1 \left( 1-\sqrt{k} \right)^4 dk \\
&& = 2\pi \int_0^1 \left( 1-4k^{\frac{1}{2}}+6k-4k^{\frac{3}{2}}+k^2 \right) dk \\
&& = 2\pi \left[k-\frac{8}{3}k^{\frac{3}{2}}+3k^2-\frac{8}{5}k^{\frac{5}{2}}+\frac{1}{3}k^3 \right]_0^1 \\
&& = 2\pi \left( 1-\frac{8}{3}+3-\frac{8}{5}+\frac{1}{3} \right) \\
&& = 2\pi \frac{60-35-24}{15}=\frac{2}{15}\pi \cdots (答)
\end{eqnarray}


