平面上の \( 3 \) 点 \( O,B,A \) が
\begin{equation}
\left| 2\vec{OA}+\vec{OB} \right| = \left| \vec{OA}+2\vec{OB} \right| =1 \\
かつ \\
(2\vec{OA}+\vec{OB})\cdot(\vec{OA}+\vec{OB})=\frac{1}{3} \\
\end{equation}
を満たすとする。
(1)\( (2\vec{OA}+\vec{OB})\cdot(\vec{OA}+2\vec{OB}) \) を求めよ。
(2)平面上の点 \( P \) が
\begin{equation}
|\vec{OP}-(\vec{OA}+\vec{OB})|\le\frac{1}{3} \\
かつ \\
\vec{OP}\cdot(2\vec{OA}+\vec{OB})\le\frac{1}{3} \\
\end{equation}
を満たすように動くとき、\( |\vec{OP}| \) の最大値と最小値を求めよ。
【解説】
\( 2\vec{OA}+\vec{OB}, \ \vec{OA}+2\vec{OB} \) の大きさがともに \( 1 \) であり、単位ベクトルになっています。(1)ではその内積を求める問題です。単位ベクトルの内積なので \( 0 \) 、すなわち直交になりそうな予感がします。\( 2\vec{OA}+\vec{OB}=\vec{u}, \ \vec{OA}+2\vec{OB}=\vec{v} \) とおき、\( \vec{u}\cdot\vec{v} \) を求めましょう。\( \vec{u}, \ \vec{v} \) が直交する単位ベクトルであることがわかります。
(2)では与えられた式を\( \vec{u}, \ \vec{v} \) を使って表します。\( \vec{u}=(1,0), \vec{v}=(0,1) \) とおいても一般性は失いませんので、その条件下で点 \( P \) が動く領域を考えてみましょう。
【解答】
(1)
\begin{equation}
\left\{
\begin{array}{ll}
2\vec{OA}+\vec{OB}=\vec{u} & \cdots ① \\
\vec{OA}+2\vec{OB}=\vec{v} & \cdots ② \\
\end{array}
\right .
\end{equation}
とおくと題意より
\begin{equation}
|\vec{u}|=1, \ |\vec{v}|=1 \ \cdots ③
\end{equation}
また①+②より
\begin{equation}
3\vec{OA}+3\vec{OB}=\vec{u}+\vec{v} \\
∴\vec{OA}+\vec{OB}=\frac{1}{3}(\vec{u}+\vec{v}) \cdots ④
\end{equation}
さらに題意より
\begin{equation}
(2\vec{OA}+\vec{OB})\cdot(\vec{OA}+\vec{OB})=\frac{1}{3} \\
\vec{u}\cdot\frac{1}{3}(\vec{u}+\vec{v})=\frac{1}{3} \\
\vec{u}\cdot(\vec{u}+\vec{v})=1 \\
|\vec{u}|^2+\vec{u}\cdot\vec{v}=1 \\
1^2+\vec{u}\cdot\vec{v}=1 \\
∴\vec{u}\cdot\vec{v}=0 \cdots ⑤
\end{equation}
よって
\begin{equation}
(2\vec{OA}+\vec{OB})\cdot(\vec{OA}+2\vec{OB})=\vec{u}\cdot\vec{v}=0 \cdots (答)
\end{equation}
(2)与えられた条件に①②を代入すると
\begin{equation}
\left\{
\begin{array}{ll}
\displaystyle \left| \vec{OP}-\frac{1}{3}(\vec{u}+\vec{v}) \right| \le \frac{1}{3} & \cdots ⑥ \\
\displaystyle \vec{OP}\cdot\vec{u} \le \frac{1}{3} & \cdots ⑦ \\
\end{array}
\right .
\end{equation}
(1)から \( |\vec{u}|=|\vec{v}|=1, \ \vec{u}\cdot\vec{v}=0 \) だから \( \vec{u}, \vec{v} \) は直交する単位ベクトルとなる。そこで、\( \vec{u}=(1,0), \vec{v}=(0,1) \) としても一般性を失わない。
③より点 \( P \) は中心 \( ( \frac{1}{3}, \frac{1}{3} ) \)、半径 \( \frac{1}{3} \) の円の周を含む内側となる。
また④より点 \( P \) を \( (x,y) \) とすると
\begin{equation}
\vec{OP}\cdot\vec{u} = (x,y)\cdot(1,0)=x\le\frac{1}{3}
\end{equation}
となるので、点 \( P \) は下図の斜線部分(境界を含む)を動く。
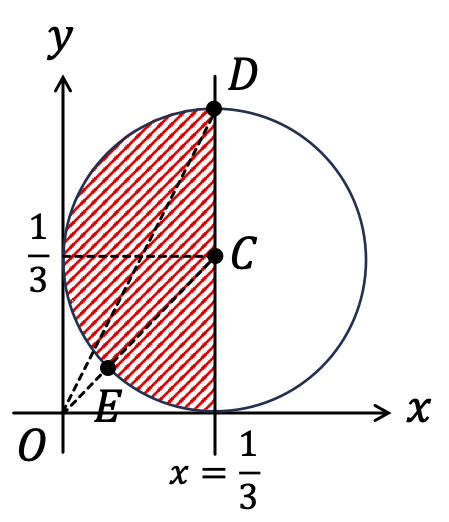
\( |\vec{OP}| \) の最小値は \( OE \) だから
\begin{eqnarray}
OE &=& \sqrt{ \left( \frac{1}{3} \right)^2 + \left( \frac{1}{3} \right)^2 }-\frac{1}{3} \\
&=& \frac{\sqrt{2}}{3}-\frac{1}{3} \\
&=& \frac{\sqrt{2}-1}{3} \cdots (答) \\
\end{eqnarray}
\( |\vec{OP}| \) の最大値は \( OD \) だから\begin{eqnarray}
OD &=& \sqrt{ \left( \frac{1}{3} \right)^2 + \left( \frac{2}{3} \right)^2 } \\
&=& \frac{\sqrt{2}}{3}-\frac{1}{3} \\
&=& \frac{\sqrt{5}}{3} \cdots (答) \\
\end{eqnarray}


