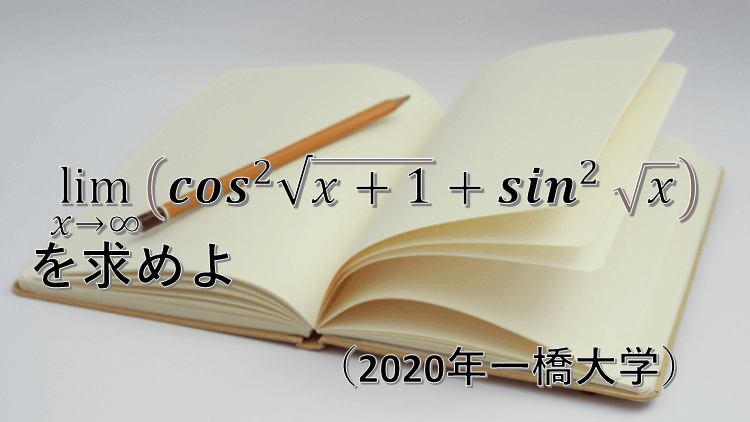$$ \lim_{ x \to \infty } ( \cos^2 \sqrt{x+1} + \sin^2 \sqrt{x} ) $$
を求めよ。
【解答】
\begin{eqnarray}
\cos^2 \sqrt{x+1} + \sin^2 \sqrt{x}
&=& \frac{1}{2} ( 1 + \cos 2 \sqrt{x+1} ) + \frac{1}{2} ( 1 – \cos 2 \sqrt{x} ) \\
&=& 1 + \frac{1}{2} ( \cos 2 \sqrt{x+1} – \cos 2 \sqrt{x} ) \\
&=& 1 + \frac{1}{2} \left\{ -2 \sin( \sqrt{x+1} + \sqrt{x} ) \cdot \sin( \sqrt{x+1} – \sqrt{x} ) \right\} \\
&=& 1 – \sin( \sqrt{x+1} + \sqrt{x} ) \cdot \sin( \sqrt{x+1} – \sqrt{x} ) \cdots ①
\end{eqnarray}
ここで \( \sqrt{x+1}+\sqrt{x} = t \) とおくと、\( x \to \infty \) のとき \( t \to \infty \) となる。また、
$$ \sqrt{x+1} – \sqrt{x} = \frac{1}{ \sqrt{x+1} + \sqrt{x} } =\frac{1}{t} $$
だから、①より
$$ \cos^2 \sqrt{x+1} + \sin^2 \sqrt{x} = 1 – \sin t \cdot \sin \frac{1}{t} \cdots ② $$
ここで、\( 0 \le | \sin t| \le 1 \) であるから、
$$ 0 \le \left| \sin t \cdot \sin \frac{1}{t} \right| = \left| \sin t \right| \left| \sin \frac{1}{t} \right| \le \left| \sin \frac{1}{t} \right| $$
となるので、
$$ 0 \le \lim_{t \to \infty} \left| \sin t \right| \left| \sin \frac{1}{t} \right| \le \lim_{t \to \infty} \left| \sin \frac{1}{t} \right| = 0 $$
となる。はさみうちの原理より、
\begin{equation}
\lim_{t \to \infty} \left| \sin t \right| \left| \sin \frac{1}{t} \right| = 0 \\
∴\lim_{t \to \infty} \sin t \cdot \sin \frac{1}{t} = 0 \cdots ③
\end{equation}
となる。よって、②③より
\begin{eqnarray}
\lim_{ x \to \infty } ( \cos^2 \sqrt{x+1} + \sin^2 \sqrt{x} )
&=& \lim_{ t \to \infty } \left( 1 – \sin t \cdot \sin \frac{1}{t} \right) \\
&=& 1 \cdots (答)
\end{eqnarray}