【問題】空間図形（2022年京都大）

【解説】

図形の問題です。\( P \) が辺 \( BC \) 上の点だから \( BP:PC= t:1-t\) とおき、\( t \) の値にかかわらず、\( \overrightarrow{PG} \) と \( \overrightarrow{OA} \) の内積が \( 0 \) になることを示せばよさそうです。しかし、\( \triangle OAP \) が \( PO=PA \) の2等辺三角形であることに気が付けば、すぐに証明できます。
また \( PG \) の長さは、\( AP \perp BC \) の時に最も短くなることに気が付けば、三平方の定理だけで求められます。

【解答】

（１）

辺 \( OA \) の中点を \( M \) とする。

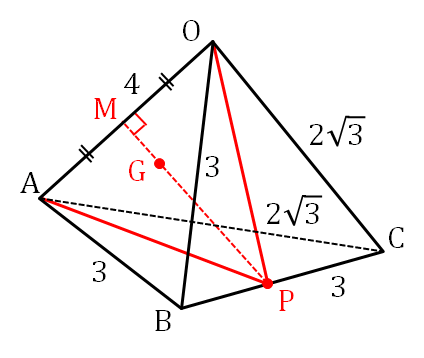
\( \triangle ABC \) と \( \triangle OBC \) において、\( AB=OB=3,\ AC=OC=2\sqrt{3}, \ BC \) は共通であり、\( 3 \) 辺の長さが等しいので \( \triangle ABC \equiv \triangle OBC \) 。 よって、
$$ \angle ABP=\angle OBP $$
また \( AB=OB=3 \)、\( BP \) は共通であるから、\( \triangle ABP \) と \( \triangle OBP \) で2辺とその間の角が等しいので \( \triangle ABP \equiv \triangle OBP \) 。よって
$$ AP=OP $$
\( \triangle APO \) は \( AP=OP \) の2等辺三角形だから、\( PM \) は辺 \( OA \) に対して、垂直二等分線となる。よって、\( \overrightarrow{PG} \perp \overrightarrow{OA} \) となる。

（２）

\( PG \) が最小となるのは、\( PM \) が最小となるときであり、\( AP \) が最小となるときである。\( \triangle ABP \) で \( AP \) の長さが最小となるのは、\( AP \perp BC \) となるときだから、

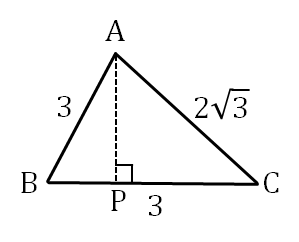
\begin{eqnarray}
AB^2 – BP^2 &=& AC^2 – CP^2 \\
3^2 – BP^2 &=& (2\sqrt{3})^2-(3-BP)^2 \\
6BP &=& 6 \\
BP &=& 1
\end{eqnarray}
\begin{eqnarray}
∴AP &=& \sqrt{AB^2-BP^2} \\
&=& \sqrt{3^2-1^2} \\
&=& 2\sqrt{2}
\end{eqnarray}
このとき、\( \triangle POA \) で

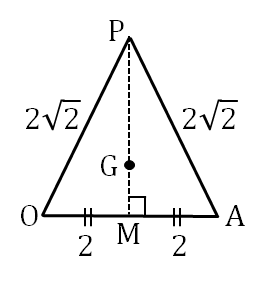
\begin{eqnarray}
PM &=& \sqrt{AP^2-AM^2} \\
&=& \sqrt{(2\sqrt{2})^2-2^2} \\
&=& 2
\end{eqnarray}
\( G \) は \( \triangle POA \) の重心だから、
\begin{eqnarray}
PG &=& \frac{2}{3} \times PM \\
&=& \frac{2}{3} \times 2 \\
&=& \frac{4}{3} \cdots （答）
\end{eqnarray}