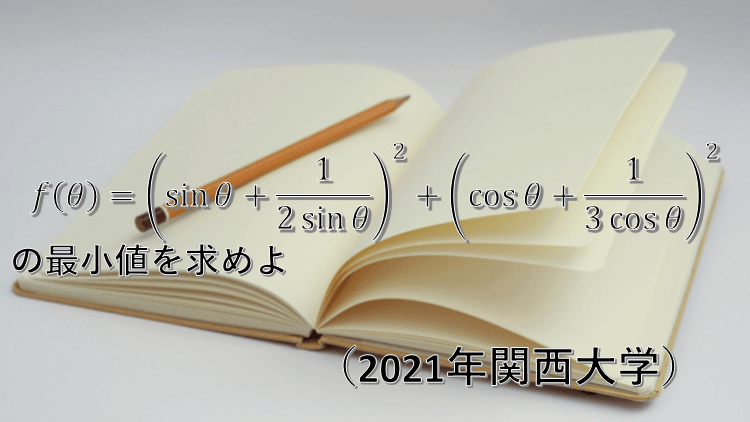【問題】微分を使って最小値を求める問題（2021年関西大学）

【解説】

微分を使って最小値を求める問題です。与えたられた式を展開して整理しましょう。三角関数を他の文字に置換すると微分しやすくなります。

【解答】

\begin{eqnarray}
f(\theta) &=& \left( \sin \theta + \frac{1}{2 \sin \theta} \right)^2 + \left( \cos \theta + \frac{1}{3 \cos \theta} \right)^2 \\
&=& \sin^2 \theta + 1 + \frac{1}{4 \sin^2 \theta} + \cos^2 \theta + \frac{2}{3} + \frac{1}{9 \cos^2 \theta} \\
&=& \frac{8}{3} + \frac{1}{4 \sin^2 \theta} + \frac{1}{9 \cos^2 \theta} \cdots ① \\
\end{eqnarray}
ここで \( \sin^2 \theta = t \) とおくと
\( \cos^2 \theta = 1 – \sin^2 \theta = 1 – t \)
また
\( 0 < \theta < \frac{\pi}{2} \) より \( 0 < \sin \theta < 1 \Leftrightarrow 0 < t < 1 \)
だから
\begin{eqnarray}
g(t) &=& \frac{1}{4 \sin^2 \theta} + \frac{1}{9 \cos^2 \theta} \\
&=& \frac{1}{4t} + \frac{1}{9(1-t)} \cdots ② \\
∴g^{\prime}(t) &=& – \frac{1}{4t^2} + \frac{1}{9(1-t)^2} \\
&=& \frac{-9(t-1)^2 + 4t^2}{36 t^2 (t-1)^2} \\
&=& – \frac{ (5t-3)(t-3) }{ 36 t^2 (t-1)^2 }
\end{eqnarray}
\( g^{\prime}(t) = 0 \) のとき \( t=-\frac{3}{5},3 \) だから
\begin{array}{c|ccccc}
\hline
t & 0 & \cdots & \frac{3}{5} & \cdots & 1 \\
\hline
g^{\prime}(t) & & – & 0 & + & \\
\hline
g(t) & & \searrow & 極小 & \nearrow & \\
\hline
\end{array}
\( t= \frac{3}{5} \) のとき、\( g(t) \) は極小かつ最小となる
\begin{eqnarray}
∴g \left( \frac{3}{5} \right) &=& \frac{1}{ \displaystyle 4 \cdot \frac{3}{5} } + \frac{1}{9 \cdot \left( \displaystyle 1 – \frac{3}{5} \right)} \\
&=& \frac{5}{12} + \frac{5}{18} \\
&=& \frac{25}{36}
\end{eqnarray}
よって①の最小値は、
\begin{eqnarray}
\frac{8}{3} + g \left( \frac{3}{5} \right) &=& \frac{8}{3} + \frac{25}{36} \\
&=& \frac{121}{36} \cdots （答）
\end{eqnarray}