【問題】三角形の形状（2021年札幌医大）

【解説】

与えられた関係式から、三角形の形を示す標準的な問題です。辺または角だけの関係式を示します。ここでは辺の関係を示します。

【解答】

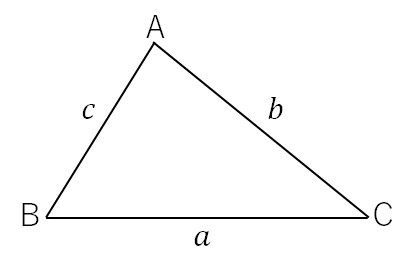
三角形 \( ABC \) の外接円の半径を \( R \) とすると、正弦定理より
\begin{equation}
\frac{b}{\sin B} = \frac{c}{\sin C} = 2R \\
∴\sin B = \frac{b}{2R} \cdots ① \\
∴\sin C = \frac{c}{2R} \cdots ② \\
\end{equation}
また余弦定理より
\begin{equation}
a^2 = b^2 + c^2 -2bc \cos A \\
\cos A = \frac{b^2+c^2-a^2}{2bc} \cdots ③
\end{equation}
①②③を与式に代入すると
\begin{equation}
\frac{c}{2R} = 2 \cdot \frac{b^2+c^2-a^2}{2bc} \cdot \frac{b}{2R} \\
c^2 = b^2+c^2-a^2 \\
a^2 = b^2 \\
a = b \\
（∵a>0, b>0）
\end{equation}
よって、三角形 \( ABC \) は、\( BC = CA \) の二等辺三角形である。