3辺AB,BC,CAの長さがそれぞれ2,3,4であるような三角形ABCを考える。P,QがABCの面積を2等分するように、それぞれ辺AB上、辺AC上を動く点とする。このとき、次の問に答えよ。
(1) cos∠BACの値を求めよ。
(2) 線分AP、線分PQの長さを、それぞれ \( x,y \) とおく。さらに \( k=x-y \) とおく。このとき、PQの長さを、\( k \) を用いて表せ。
(3) PQの長さの最大値と最小値を求めよ。
【解答】
(1)
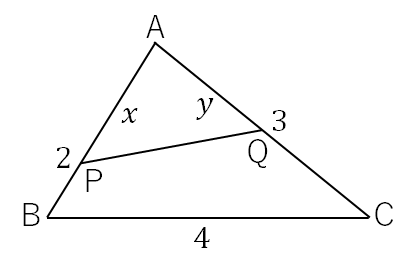
△ABCで余弦定理より
\begin{eqnarray}
BC^2 &=& AB^2+AC^2-2AB \cdot AC \cos \angle BAC \\
∴\cos \angle BAC &=& \frac{ AB^2+AC^2-BC^2 }{ 2AB \cdot AC } \\
&=& \frac{2^2+3^2-4^2}{2 \cdot2 \cdot 3} \\
&=& -\frac{1}{4} \cdots (答)
\end{eqnarray}
(2)題意より
\begin{eqnarray}
\triangle APQ &=& \frac{1}{2} \triangle ABC \\
\frac{1}{2}AP \cdot AQ \sin \angle PAQ &=& \frac{1}{2} \cdot \frac{1}{2}AB \cdot AC \sin \angle BAC \\
\frac{1}{2} \cdot x \cdot y \cdot \sin \angle BAC &=& \frac{1}{2} \cdot \frac{1}{2} \cdot 2 \cdot 3 \cdot \sin \angle BAC \\
∴xy &=& 3 \cdots ①
\end{eqnarray}
また、\( \triangle APQ \) で余弦定理より
\begin{eqnarray}
PQ^2 &=& AP^2 + AQ^2 – 2 AP \cdot AQ \cos \angle PAQ \\
&=& x^2 + y^2 – 2xy \cdot \left(-\frac{1}{4} \right) \\
&=& (x-y)^2 + \frac{5}{2}xy \\
&=& k^2 + \frac{15}{2} (∵①より)\\
∴PQ &=& \sqrt{k^2+\frac{15}{2}} \cdots (答)
\end{eqnarray}
(3)(2)の結果より \( x,y \) は
\begin{equation}
\left\{
\begin{array}{l}
\displaystyle xy=3 \Leftrightarrow y=\frac{3}{x} \\
x \le 2 \\
y \le 3
\end{array}
\right .
\end{equation}
を満たさなければならない。
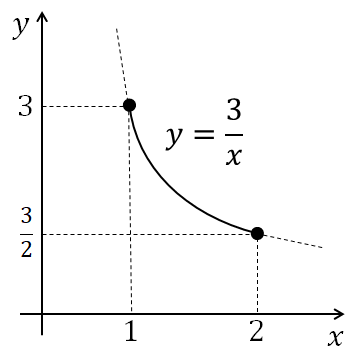
グラフより \( x,y \) がとりうる範囲は
\begin{equation}
\left\{
\begin{array}{l}
1 \le x \le 2 \\
\frac{3}{2} \le y \le 3
\end{array}
\right . \\
∴-2 \le x-y \le \frac{1}{2} \\
-2 \le k \le \frac{1}{2} \\
∴ 0 \le k^2 \le 4
\end{equation}
(2)の結果より
\begin{equation}
\begin{array}{ll}
k^2=0 のとき & 最小値 \displaystyle \sqrt{0+\frac{15}{2}} = \frac{\sqrt{30}}{2} \\
k^2=4 のとき & 最大値 \displaystyle \sqrt{4+\frac{15}{2}} = \frac{\sqrt{46}}{2}
\end{array}
\cdots (答)
\end{equation}


