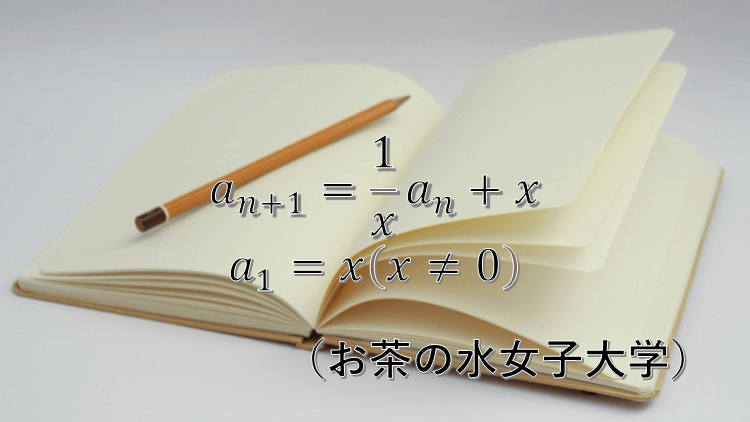【問題】漸化式を求める（お茶の水女子大）

漸化式に文字を含む問題です。特性方程式で \( \alpha \) を求める際、文字列での割算に注意しましょう。

【解答】
$$ a_{n+1}=\frac{1}{x}a_n + x \cdots ①$$
まず①の特性方程式を考える。
\begin{eqnarray}
\alpha &=& \frac{1}{x} \alpha + x \cdots ② \\
\left( 1-\frac{1}{x} \right) \alpha &=& x \\
\frac{x-1}{x} \alpha &=& x \cdots ③
\end{eqnarray}

i)　\( x \ne 1 \) のとき、③より
$$ \alpha = \frac{x^2}{x-1} $$
①ー②より
$$ a_{n+1}-\alpha = \frac{1}{x}(a_n -\alpha) $$
数列 \( \{ a_n -\alpha \} \) は、初項 \( a_1-\alpha \)、公比 \( \displaystyle \frac{1}{x} \) の等比数列だから、
\begin{eqnarray}
a_n – \alpha &=& (a_1 – \alpha ) \left( \frac{1}{x} \right)^{n-1} \\
a_n &=& \alpha + (a_1 – \alpha ) \frac{1}{x^{n-1}} \\
&=& \frac{x^2}{x-1} + \left( x – \frac{x^2}{x-1} \right) \frac{1}{x^{n-1}} \\
&=& \frac{x^2}{x-1} – \frac{x}{x-1} \frac{1}{x^{n-1}} \\
&=& \frac{x^n-1}{x^{n-2}(x-1)} \\
\end{eqnarray}

ii)　\( x=1 \) のとき、①より
\begin{eqnarray}
a_{n+1} = a_n+1
\end{eqnarray}
数列 \( \{ a_n \}\) は初項 \( a_1=1 \)、公差 \( 1 \) の等差数列だから、
$$ a_n = 1+(n-1) \times 1 = n $$

i)、ii)より
\begin{equation}
\left\{
\begin{array}{ll}
x \ne 1 のとき & a_n = \displaystyle \frac{x^n-1}{x^{n-2}(x-1)} \\
x=1の とき & a_n=n
\end{array}
\right.
\end{equation}