\( 1 \) 辺の長さが \( 1 \) の正四面体に内接する球 \( O_1 \) の半径は \( \fbox{①} \) であり、同じ正四面体に外接する球 \( O_2 \) の半径は \( \fbox{②} \) である。従って、球 \( O_2 \) の体積は球 \( O_1 \) の体積の \( \fbox{③} \) 倍である。
【解説】
正四面体の内接球、外接球の半径を求める問題です。中学生の知識で求めることができます。問題を通して、導出方法を身につけましょう。内接球の半径は、体積を使って求めます。別解で示した関係も是非、参照してください。
【解答】
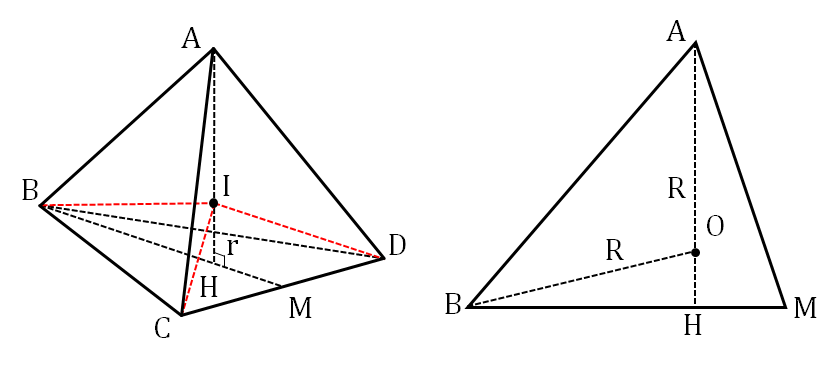
正四面体 \( ABCD \) を考える。\( CD \) の中点を \( M \)、\( A \) から底面 \( BCD \) におろした垂線との交点を \( H \) とする。\( H \) は \( \triangle BCD \) の重心となるので、
\begin{equation}
BH = \frac{2}{3}BM = \frac{2}{3} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{3} \\
\end{equation}
\( \triangle ABH \) で三平方の定理より
\begin{equation}
AH^2 = AB^2 – BH^2 = 1^2 – \left( \frac{\sqrt{3}}{3} \right)^2 =\frac{2}{3} \\
∴AH = \frac{\sqrt{6}}{3} \\
\end{equation}
正四面体 \( ABCD \) の体積 \( V \) は
\begin{eqnarray}
V &=& \frac{1}{3} \triangle BCD \cdot AH \\
&=& \frac{1}{3} \cdot \left( \frac{1}{2} \times \frac{\sqrt{3}}{2} \times 1 \right) \cdot \frac{\sqrt{6}}{3} \\
&=& \frac{1}{3} \times \frac{\sqrt{3}}{4} \times \frac{\sqrt{6}}{3} \\
&=& \frac{\sqrt{2}}{12} \cdots ①
\end{eqnarray}
ここで内接球の中心を \( I \) 、半径を \( r \) とする。正四面体 \( ABCD \) は 三角すい \( I-BCD \) の\( 4 \) 倍となるので、
\begin{eqnarray}
V &=& 4 \times \frac{1}{3} \triangle BCD \cdot r = 4 \times \frac{1}{3} \times \frac{\sqrt{3}}{4} \times r \\
&=& \frac{\sqrt{3}}{3} r \cdots ②
\end{eqnarray}
①②より
\begin{equation}
\frac{\sqrt{3}}{3} r = \frac{\sqrt{2}}{12} \\
∴r=\frac{\sqrt{6}}{12} \cdots (答)
\end{equation}
次に外接球の中心を \( O \)、半径を \( R \) とする。\( \triangle OBH \) で三平方の定理より
\begin{equation}
OB^2 = BH^2 + OH^2 \\
R^2 = \left( \frac{2}{3} \times \frac{\sqrt{3}}{2} \right)^2 + \left( \frac{\sqrt{6}}{3} – R \right)^2 \\
R^2 = \frac{1}{3} + \frac{2}{3} – \frac{2\sqrt{6}}{3}R + R^2 \\
\frac{2\sqrt{6}}{3}R = 1 \\
∴R = \frac{\sqrt{6}}{4} \cdots (答)
\end{equation}
内接球 \( O_1 \) の体積を \( V_1 \)、外接球 \( O_2 \) の体積を \( V_2 \) とすると、
\begin{eqnarray}
V_1 : V_2 &=& r^3 : R^3 \\
&=& \left( \frac{\sqrt{6}}{12} \right)^3 : \left( \frac{\sqrt{6}}{4} \right)^3 \\
&=& \left( \frac{1}{3} \right) ^3 : 1^3 \\
&=& 1:27
\end{eqnarray}
よって、\( O_2 \) の体積は \( O_1 \) の \( 27 \) 倍となる。
【別解】
正四面体の内接球と外接球の中心は一致し、\( AI:IH=3:1 \) となる。これは以下で証明できます。
\begin{equation}
AI = AH -r = \frac{\sqrt{6}}{3} – \frac{\sqrt{6}}{12} = \frac{\sqrt{6}}{4} \\
AO = R = \frac{\sqrt{6}}{4} = AI
\end{equation}
となり、点 \( I \) と点 \( O \) は一致する。また
\begin{equation}
AI:IH = \frac{\sqrt{6}}{4} : \frac{\sqrt{6}}{12} = 3:1
\end{equation}
となる。
上記を利用すると、
\begin{equation}
r=\frac{1}{4}AH=\frac{1}{4} \times \frac{\sqrt{6}}{3}=\frac{\sqrt{6}}{12} \\
R=\frac{3}{4}AH=\frac{3}{4} \times \frac{\sqrt{6}}{3} = \frac{\sqrt{6}}{4}
\end{equation}
と求めることができます。


