(1) \( \displaystyle \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{k} \) を求めよ。
(2) 任意の正数 \( a \) に対して \( \displaystyle \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{a+k} \) は(1)と同じ極限をもつことを証明せよ。
【解説】
(1)は区分求積法を使うと求めることができますが、\( k \) の範囲が通常と違います。注意してください。(2)でははさみうちの原理を使います。下限の設定方法では、グラフを使うと考えやすいです。
$$ \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k=0}^{n} f \left( \frac{k}{n} \right) = \int_0^1 f(x) dx $$
$$ \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k=n}^{2n} f \left( \frac{k}{n} \right) = \int_1^2 f(x) dx $$
【解答】
(1)
\begin{eqnarray}
\lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{k}
&=& \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k=n}^{2n} \frac{1}{\frac{k}{n}} \\
&=& \int_{1}^{2} \frac{1}{x} dx \\
&=& \left[\log |x| \right]_1^2 \\
&=& \log 2 \cdots (答)
\end{eqnarray}
(2) 下図より
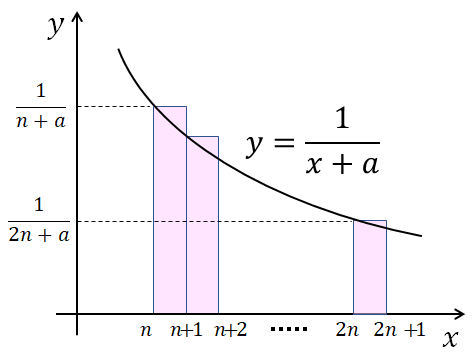
\begin{equation}
\int_{n}^{2n+1} \frac{1}{x+a} dx < \sum_{k=n}^{2n} \frac{1}{k+a} \\
∴ \lim_{n \rightarrow \infty} \int_{n}^{2n+1} \frac{1}{x+a} dx < \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{k+a} \cdots ①
\end{equation}
①の左辺は
\begin{eqnarray}
\lim_{n \rightarrow \infty} [ \log |x+a| ]_{n}^{2n+1} &=& \lim_{n \rightarrow \infty} \log \frac{2n+a+1}{n+a} \\
&=& \log 2
\end{eqnarray}
となるから
$$ \log 2 < \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{k+a} \cdots ② $$
また \( \frac{1}{a+k} < \frac{1}{k} \) だから
\begin{equation}
\sum_{k=n}^{2n} \frac{1}{a+k} < \sum_{k=n}^{2n} \frac{1}{k} \\
\lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{a+k} < \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{k} \\
∴ \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{a+k} < \log 2 \cdots ③ \\
(∵(1)より)
\end{equation}
②③より、はさみうちの原理から
$$ \lim_{n \rightarrow \infty} \sum_{k=n}^{2n} \frac{1}{a+k} = \log 2 $$
となり、(1)と同じ極値をとる(証明終了)


-120x68.png)