複素数 \( \alpha, \beta, \gamma \) が \( |\alpha|=|\beta|=|\gamma|=1 \) かつ \( |\alpha|+|\beta|+|\gamma=0 \) を満たすとき、以下の問に答えよ。
(1)\( \alpha, \beta, \gamma \) を表す複素平面上の点が正三角形をなすことを示せ。
(2)\( \displaystyle \frac{\alpha\beta}{\gamma^2}+\frac{\beta\gamma}{\alpha^2}+\frac{\gamma\alpha}{\beta^2} \) の値を求めよ。
(3)\( n \) が \( 3 \) で割り切れない自然数とするとき \( \alpha^n+\beta^n+\gamma^n \) の値を求めよ。
【解説】
\( |\alpha|=|\beta|=|\gamma|=1 \) は原点が外心、\( |\alpha|+|\beta|+|\gamma=0 \) は原点が重心であることを示しています。外心と重心が一致する三角形は正三角形ですね。
もう少し汎用的に表現すると、重心、内心、外心、垂心のうち2つが一致する三角形は正三角形となります。
【解答】
(1)\( 原点O、A(\alpha)、B(\beta)、C(\gamma)\) とし \( \triangle ABC \) が正三角形であることを示す。
\( \overrightarrow{OA}=\overrightarrow{a}, \ \overrightarrow{OB}=\overrightarrow{b}, \ \overrightarrow{OC}=\overrightarrow{c} \) とおくと、
\begin{eqnarray}
| \overrightarrow{a} | &=& | \alpha | = 1 \\
| \overrightarrow{b} | &=& | \beta | = 1 \\
| \overrightarrow{c} | &=& | \gamma | = 1 \\
| \overrightarrow{a}+\overrightarrow{b} | &=& | \alpha+\beta | \\
&=& | -\gamma | = 1
\end{eqnarray}
ここで
\begin{eqnarray}
|\overrightarrow{a}+\overrightarrow{b}|^2
&=& |\overrightarrow{a}|^2 + 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 \\
\overrightarrow{a} \cdot \overrightarrow{b} &=& -\frac{1}{2}
\end{eqnarray}
となるので、
\begin{eqnarray}
\cos \angle AOB &=& \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|} \\
&=& -\frac{1}{2} \\
∴\angle AOB &=& 120^{\circ}
\end{eqnarray}
同様にして、\( \angle AOB = \angle BOC = \angle COA = 120^{\circ} \) となり、2辺とその間の角が等しいので、\( \triangle AOB \equiv \triangle BOC \equiv \triangle COA \) となる。
よって、\( AB=BC=CA \) であるから、 \( \triangle ABC \) は正三角形となり、 複素数 \( \alpha, \beta, \gamma \) が表す点は正三角形となる。
(2)
\begin{eqnarray}
\frac{\alpha\beta}{\gamma^2}+\frac{\beta\gamma}{\alpha^2}+\frac{\gamma\alpha}{\beta^2}
&=& \frac{\alpha^3 \beta^3 + \beta^3 \gamma^3 + \gamma^3 \alpha^3}{\alpha^2 \beta^2 \gamma^2} \cdots ①
\end{eqnarray}
ここで、\( \alpha, \beta, \gamma \) が表す点は正三角形だから、
\begin{eqnarray}
\beta &=& \alpha \left( \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3} \right) \\
\gamma &=& \alpha \left\{ \cos \left(-\frac{2\pi}{3}\right) + i \sin \left(-\frac{2\pi}{3}\right) \right\}
\end{eqnarray}
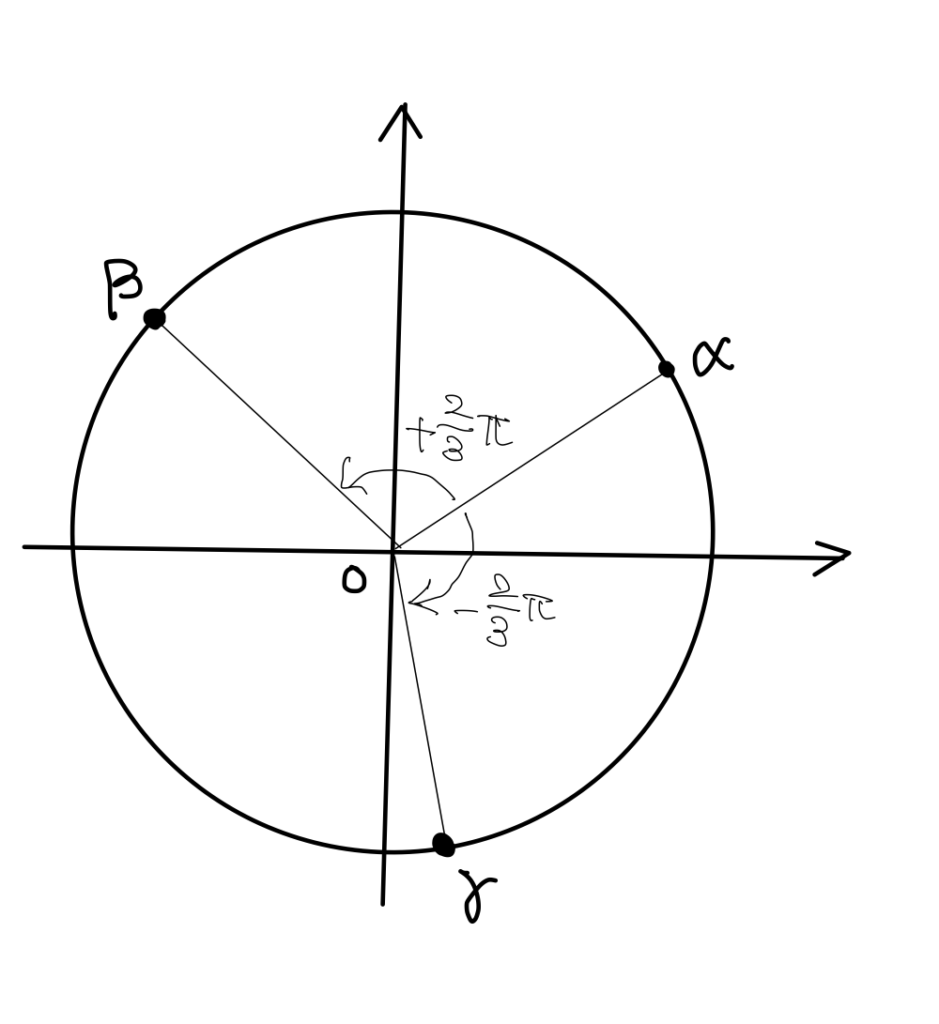
とおくと、
\begin{eqnarray}
\beta^3 &=& \alpha^3 \left( \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3} \right)^3 \\
&=& \alpha^3 ( \cos 2\pi + i \sin 2\pi ) \\
&=& \alpha^3 \cdots ② \\[10pt]
\gamma^3 &=& \alpha^3 \left\{ \cos \left(-\frac{2\pi}{3}\right) + i \sin \left(-\frac{2\pi}{3}\right) \right\}^3 \\
&=& \alpha^3 \{ \cos (-2\pi) + i \sin (-2\pi) \} \\
&=& \alpha^3 \cdots ③ \\[10pt]
\beta^2 \gamma^2 &=& (\beta \gamma)^2 \\
&=& \alpha^2 \left( \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3} \right) \\
&& \hspace{10pt} \times \left\{ \cos \left(-\frac{2\pi}{3}\right) + i \sin \left(-\frac{2\pi}{3}\right) \right\} \\
&=& \alpha^2 \cdots ④
\end{eqnarray}
②~④を①に代入すると
\begin{eqnarray}
(与式) &=& \frac{\alpha^6 + \alpha^6 + \alpha^6 }{\alpha^2 \cdot \alpha^2 \cdot \alpha^2 } \\
&=& \frac{3\alpha^6}{\alpha^6} \\
&=& 3 \cdots (答)
\end{eqnarray}(3)
\begin{eqnarray}
\beta^n &=& \alpha^n \left( \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3} \right)^n \\
&=& \alpha^n \left( \cos \frac{2n\pi}{3} + i \sin \frac{2n\pi}{3} \right) \cdots ⑤ \\[10pt]
\gamma^n &=& \alpha^n \left\{ \cos \left(-\frac{2\pi}{3}\right) + i \sin \left(-\frac{2\pi}{3}\right) \right\}^n \\
&=& \alpha^n \left\{ \cos \left(-\frac{2n\pi}{3}\right) + i \sin \left(-\frac{2n\pi}{3}\right) \right\} \\
&=& \alpha^n \left( \cos \frac{2n\pi}{3} – i \sin \frac{2n\pi}{3} \right) \cdots ⑥
\end{eqnarray}
⑤⑥より
\begin{eqnarray}
\alpha^n + \beta^n + \gamma^n &=& \alpha^n + 2 \alpha^n \cos \frac{2n\pi}{3} \cdots ⑦
\end{eqnarray}
ここで \( n \) は \( 3 \) で割り切れない自然数だから、\( n = 3k \pm 1\) とおけるので、
\begin{eqnarray}
\cos \frac{2n\pi}{3} &=& \cos \left( 2n\pi \pm \frac{2\pi}{3} \right) \\
&=& \cos \left( \pm \frac{2\pi}{3} \right) \\
&=& -\frac{1}{2} \cdots ⑧
\end{eqnarray}
⑧を⑦に代入すると、
\begin{eqnarray}
\alpha^n + \beta^n + \gamma^n &=& \alpha^n + 2 \alpha^n \times \left( -\frac{1}{2} \right) \\
&=& \alpha^n – \alpha^n \\
&=& 0 \cdots (答)
\end{eqnarray}


