\( 2 \) 以上の自然数 \( n \) に対して、不等式
$$ \frac{1}{2^3} + \frac{1}{3^3} + \frac{1}{4^3} + \cdots + \frac{1}{n^3} < \frac{1}{4} $$
を示せ
【解説】
左辺の式を見たとき、\( y=\frac{1}{x^3} \) のグラフを使って面積の大小比較をイメージできるかがポイントです。今回の問題では、如何にして \( \frac{1}{4} \) を作り出すかで悩んでしまいます。
【解答】
左辺の \( \displaystyle \sum_{k=2}^{n} \frac{1}{k^3} \) を評価するにあたり、\( y=\frac{1}{x^3} \) のグラフを考える。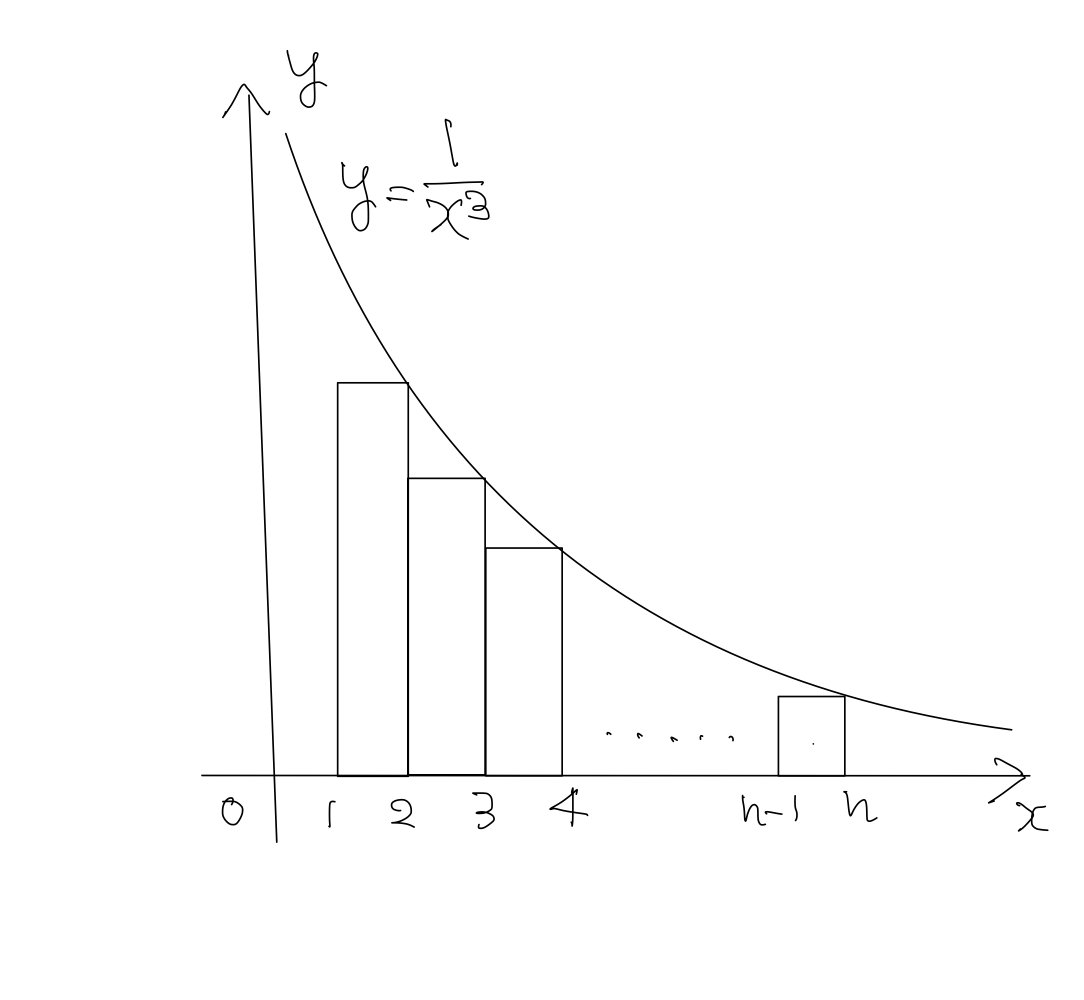
\begin{eqnarray}
\sum_{k=2}^{n} \frac{1}{k^3} &<& \frac{1}{2^3} + \int_{2}^{n} \frac{1}{x^3} dx \cdots ① \\
&=& \frac{1}{8} + \left[ – \frac{1}{2} \cdot \frac{1}{x^2} \right]_{2}^{n} \\
&=& \frac{1}{8} – \frac{1}{2} \left( \frac{1}{n^2} – \frac{1}{4} \right) \\
&=& \frac{1}{4} – \frac{1}{2n^2} \\
&<& \frac{1}{4}
\end{eqnarray}
よって、\( \displaystyle \sum_{k=2}^{n} \frac{1}{k^3} < \frac{1}{4} \) となる。
(補足)①を以下のように面積を比較してしまうと、\( \displaystyle \frac{1}{4} \) を導けません。
\begin{eqnarray}
\sum_{k=2}^{n} \frac{1}{k^3} &<& \int_{1}^{n} \frac{1}{x^3} dx = \frac{1}{2} – \frac{1}{2n^2}
\end{eqnarray}
【別解】
\begin{eqnarray}
n^3 – (n-1)n(n+1) &=& n^3 -( n^3 -n ) \\
&=& n > 0
\end{eqnarray}
\begin{eqnarray}
∴n^3 &>& (n-1)n(n+1) \\
∴\frac{1}{n^3} &<& \frac{1}{(n-1)n(n+1)} \\
&=& \frac{1}{2} \left\{ \frac{1}{(n-1)n} – \frac{1}{n(n+1)} \right\} \cdots ②
\end{eqnarray}
②の結果より
\begin{eqnarray}
\sum_{k=2}^{n} \frac{1}{k^3}
&<& \frac{1}{2} \left[ \left\{ \frac{1}{1 \cdot 2} – \frac{1}{2 \cdot 3} \right\} + \left\{ \frac{1}{2 \cdot 3} – \frac{1}{3 \cdot 4} \right\} + \cdots \right. \\
&& \left. \hspace{20pt} \cdots + \left\{ \frac{1}{(n-1) \cdot n} – \frac{1}{n \cdot (n+1)} \right\} \right] \\
&=& \frac{1}{2} \left\{ \frac{1}{2} – \frac{1}{n(n+1)} \right\} \\
&=& \frac{1}{4} – \frac{1}{2n(n+1)} \\
&<& \frac{1}{4} \cdots (証明終了)
\end{eqnarray}


