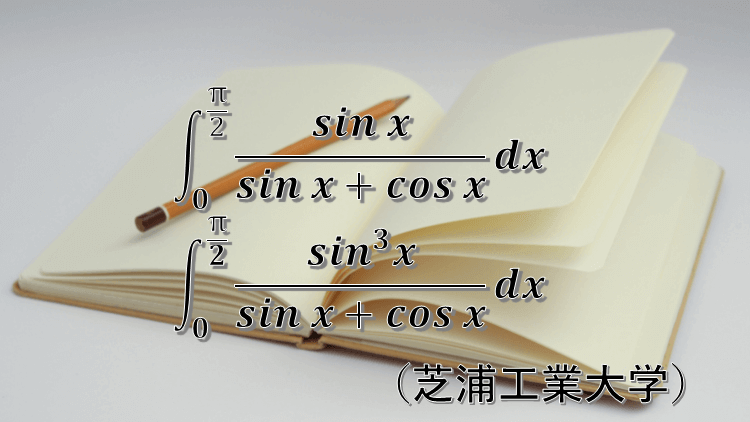(1) \( \displaystyle \int_{0}^{\frac{\pi}{2}} \frac{\sin x}{\sin x + \cos x} dx = \int_{0}^{\frac{\pi}{2}} \frac{\cos x}{\sin x + \cos x} dx \) となることを示し、この式の値を求めよ。
(2) \( \displaystyle \int_{0}^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx \) の値を求めよ。
【解答】
(1)\( \frac{\pi}{2}-x=t \) とおくと、
\begin{equation}
x=\frac{\pi}{2}-t \\
∴dx=-dt \\
\begin{array}{c|ccc}
x & 0 & \to & \frac{\pi}{2} \\
\hline
t & \frac{\pi}{2} & \to & 0 \\
\end{array}
\end{equation}
また、
\begin{eqnarray}
\sin ( \frac{\pi}{2} – t ) = \cos t,\ \cos ( \frac{\pi}{2} – t ) = \sin t
\end{eqnarray}
だから
\begin{eqnarray}
I &=& \int_{0}^{\frac{\pi}{2}} \frac{\sin x}{\sin x + \cos x} dx \\
&=& \int_{\frac{\pi}{2}}^{0} \frac{\sin ( \frac{\pi}{2} – t )}{\sin ( \frac{\pi}{2} – t ) + \cos ( \frac{\pi}{2} – t )} (-dt) \\
&=& – \int_{\frac{\pi}{2}}^{0} \frac{\cos t}{\cos t + \sin t} dt \\
&=& \int_{0}^{\frac{\pi}{2}} \frac{\cos x}{\cos x + \sin x} dx
\end{eqnarray}
となる。
\begin{eqnarray}
2I &=& \int_{0}^{\frac{\pi}{2}} \frac{\sin x}{\sin x + \cos x} dx + \int_{0}^{\frac{\pi}{2}} \frac{\cos x}{\sin x + \cos x} dx \\
&=& \int_{0}^{\frac{\pi}{2}} \frac{\sin x + \cos x}{\sin x + \cos x} dx \\
&=& \int_{0}^{\frac{\pi}{2}} dx \\
&=& [ x ]_{0}^{\frac{\pi}{2}} \\
&=& \frac{\pi}{2} \\
∴I &=& \frac{\pi}{4} \cdots (答)
\end{eqnarray}
(2)\( \frac{\pi}{2}-x=t \) とおき、(1)と同様に置換すると、
\begin{eqnarray}
J &=& \int_{0}^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx \\
&=& \int_{\frac{\pi}{2}}^{0} \frac{\sin^3 (\frac{\pi}{2}-t)}{\sin (\frac{\pi}{2}-t) + \cos (\frac{\pi}{2}-t) } (-dt) \\
&=& – \int_{\frac{\pi}{2}}^{0} \frac{\cos^3 t}{\cos t + \sin t } dt \\
&=& \int_{0}^{\frac{\pi}{2}} \frac{\cos^3 x}{\cos x + \sin x } dx
\end{eqnarray}
となる。
\begin{eqnarray}
2J &=& \int_{0}^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx + \int_{0}^{\frac{\pi}{2}} \frac{\cos^3 x}{\cos x + \sin x } dx \\
&=& \int_{0}^{\frac{\pi}{2}} \frac{\sin^3 x + \cos^3 x}{\sin x + \cos x} dx \\
&=& \int_{0}^{\frac{\pi}{2}} \frac{(\sin x + \cos x)(\sin^2 x – \sin x \cos x +\cos^2 x)}{\sin x + \cos x} dx \\
&=& \int_{0}^{\frac{\pi}{2}} \left(1 – \sin x \cos x \right) dx \\
&=& \int_{0}^{\frac{\pi}{2}} \left(1 – \frac{1}{2}\sin 2x \right) dx \\
&=& \left[ x + \frac{1}{4} \cos 2x \right]_{0}^{\frac{\pi}{2}} \\
&=& \left( \frac{\pi}{2} – 0 \right) + \frac{1}{4} \left( – 1 – 1 \right) \\
&=& \frac{\pi}{2} -\frac{1}{2} \\
∴J &=& \frac{\pi}{4} -\frac{1}{4} \cdots (答)
\end{eqnarray}